数据结构与算法

计算机与安全理论
发布日期:   2023-02-15
更新日期:   2024-07-23
文章字数:   2.3k
阅读时长:   8 分

【算法】图的邻接矩阵：$K$顶点

（2023年408统考第41题，13分）
已知有向图$G$采用邻接矩阵存储，定义如下：

1
2
3
4
5
typedef struct{                                      //图的定义
	int numVertices, numEdges;                       //图中实际的顶点数和边数
	char VerticesList[MAXV];                         //顶点表，MAXV为已定义常数
	int Edge[MAXV][MAXV];                            //边表
}MGraph;

将图中出度大于入度的顶点称为$K$顶点。例如，下图中结点$a$和结点$b$均为$K$顶点。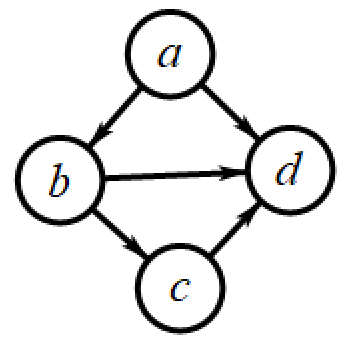

请设计算法int printVertices(MGraph G)，对任意给定的非空有向图$G$，输出$G$中所有$K$顶点，并返回$K$顶点的个数。
（1）给出算法的基本思想；（2）根据设计思想，采用C或C++语言描述算法，关键之处给出注释。

邻接矩阵中第$i$行之和即为第$i$个顶点的出度，第$i$列之和即为第$i$个顶点的入度。因此，只要分别按行按列遍历图$G$的邻接矩阵，即可求出每个顶点的入度和出度。如果一个顶点的出度大于入度，则将该$K$顶点输出，计数器加一。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int printVertices(MGraph G){                      //打印图G的所有K顶点并计数
	int i, j;
	int inDegree, outDegree;
	int count = 0;
	for(i=0;i<G.numVertices;++i){                 //遍历图的顶点
		inDegree = 0;                             //初始化顶点的入度
		outDegree = 0;                            //初始化顶点的出度
		for(j=0;j<G.numVertices;++j){
			if(G.Edge[i][j]==1) outDegree++;      //有结点i到结点j的边，出度加一
			if(G.Edge[j][i]==1) inDegree++;       //有结点j到结点i的边，入度加一
		}
		if(outDegree>inDegree){                   //出度大于入度的顶点是K顶点
			printf("%s是K顶点\n",G.VerticeList[i]);
			                                      //输出K顶点
			count++;                              //计数器的值加一
		}                    
	}
	return count;
}
  1. 时间复杂度O($n^2$)，空间复杂度O(1)；
  2. vertex(pl. vertices) n.顶点、头顶、天顶；
  3. 以上代码来源于ChatGPT，有删改。

【算法】外部排序：置换-选择算法

（2023年408统考第42题，10分）
对含有$n$（$n>0$）个记录的文件进行外部排序，采用置换-选择算法生成初始归并段时需要使用一个工作区，工作区中能保存$m$个记录，请回答下列问题：
（1）若$n=19$，文件记录的关键字是：51、94、37、92、14、63、15、99、48、56、23、60、31、17、43、8、90、166、100。当$m=4$时，可以生成几个初始归并段，每个初始归并段中的内容是什么？
（2）对于任意的$n\gg m>0$，求生成的第一个归并段的长度的最大值和最小值。

前情提要：为什么我们需要置换-选择算法？

外部排序的时间开销主要花费在磁盘块的读写过程中，所以减少归并趟数$S$，就能减少读写磁盘的次数，从而提高外部排序的速度。可以求得$S=\lceil \log_{k}r \rceil$，其中$k$是归并路数，$r$是初始归并段的长度。因此，通过败者树可以增大归并路数$k$，通过置换选择排序生成更长的初始归并段可以减小$r$，在初始归并段长度不等的情况下使用最佳归并树，均可以减少$S$的值。

而$r=\lceil \frac{n}{l} \rceil$，其中$n$是记录数，$l$是每个归并段的长度。$n$由文件的客观属性决定，无法改变；而置换选择算法增大了$l$，相较于不使用置换-选择排序算法，其$l$平均增加了一倍。因此，我们需要置换-选择算法提高外部排序的速度。

置换-选择算法的步骤如下：

  1. 从文件中（从前往后地）输入记录到内存工作区中，直至内存工作区满或者文件中不再含有记录；
  2. 记MINIMAX为工作区中的最小元素；
  3. 将MINIMAX输出；
  4. 若仍有记录未输入进工作区，则从文件中输入一个记录进入内存工作区中；
  5. 从内存工作区中找出不小于MINIMAX的最小元素，输出该元素并把该元素记为MINIMAX；
  6. 重复第3步至第5步，直至内存工作区中所有元素均小于MINIMAX。一个归并段生成，MINIMAX重置。
  7. 重复第2步至第6步，直至内存工作区中没有元素，置换选择排序算法结束。

以第（1）问作为例子来熟悉置换-选择排序。

  • 读入前4条记录，此时工作区中的内容为：51、94、37、92，取MINIMAX=37，把37输出到第一个归并段；

  • 读入14，此时工作区中的内容为：51、94、14、92，不小于MINIMAX=37的最小元素是51，取MINIMAX=51，把51输出到第一个归并段；

  • 读入63，此时工作区中的内容为：63、94、14、92，不小于MINIMAX=51的最小元素是63，取MINIMAX=63，把63输出到第一个归并段；

  • 读入15，此时工作区中的内容为：15、94、14、92，不小于MINIMAX=63的最小元素是92，取MINIMAX=92，把92输出到第一个归并段；

  • 读入99，此时工作区中的内容为：15、94、14、99，不小于MINIMAX=92的最小元素是94，取MINIMAX=94，把94输出到第一个归并段；

  • 读入48，此时工作区中的内容为：15、48、14、99，不小于MINIMAX=94的最小元素是99，取MINIMAX=99，把99输出到第一个归并段；

  • 读入56，此时工作区中的内容为：15、48、14、56，工作区中没有不小于MINIMAX=99的元素。第一个归并段完成，其内容为：37、51、63、92、94、99。

  • 此时工作区中的内容为：15、48、14、56，取MINIMAX=14，把14输出到第二个归并段；

  • 读入23，此时工作区中的内容为：15、48、23、56，不小于MINIMAX=14的最小元素是15，取MINIMAX=15，把15输出到第二个归并段；

  • 读入60，此时工作区中的内容为：60、48、23、56，不小于MINIMAX=15的最小元素是23，取MINIMAX=23，把23输出到第二个归并段；

  • 读入31，此时工作区中的内容为：60、48、31、56，不小于MINIMAX=23的最小元素是31，取MINIMAX=31，把31输出到第二个归并段；

  • 读入17，此时工作区中的内容为：60、48、17、56，不小于MINIMAX=31的最小元素是48，取MINIMAX=48，把48输出到第二个归并段；

  • 读入43，此时工作区中的内容为：60、43、17、56，不小于MINIMAX=48的最小元素是56，取MINIMAX=56，把56输出到第二个归并段；

  • 读入8，此时工作区中的内容为：60、43、17、8，不小于MINIMAX=56的最小元素是60，取MINIMAX=60，把60输出到第二个归并段；

  • 读入90，此时工作区中的内容为：90、43、17、8，不小于MINIMAX=60的最小元素是90，取MINIMAX=90，把90输出到第二个归并段；

  • 读入166，此时工作区中的内容为：166、43、17、8，不小于MINIMAX=90的最小元素是166，取MINIMAX=166，把166输出到第二个归并段；

  • 读入100，此时工作区中的内容为：100、43、17、8，工作区中没有不小于MINIMAX=166的元素。第二个归并段完成，其内容为：14、15、23、31、48、56、60、90、166。

  • 此时工作区中的内容为：100、43、17、8，所有数据均已进入工作区。取MINIMAX=8，把8输出到第三个归并段；

  • 此时工作区中的内容为：100、43、17、$\varnothing$，取MINIMAX=17，把17输出到第三个归并段；

  • 此时工作区中的内容为：100、43、$\varnothing$、$\varnothing$，取MINIMAX=43，把43输出到第三个归并段；

  • 此时工作区中的内容为：100、$\varnothing$、$\varnothing$、$\varnothing$，取MINIMAX=100，把100输出到第三个归并段；

  • 此时工作区空空如也：$\varnothing$、$\varnothing$、$\varnothing$、$\varnothing$，第三个归并段完成，其内容为：8、17、43、100，置换-选择算法也结束了。

故第（1）问的答案为：生成3个初始归并段，第一个初始归并段为：37、51、63、92、94、99；第二个初始归并段为：14、15、23、31、48、56、60、90、166；第三个初始归并段为：8、17、43、100。

对于第（2）问，考虑极端情况。

若原来的文件已经正序，即$x_1 \leq x_2 \leq \cdots \leq x_n$，则将$x_i$作为MINIMAX时，后面的元素均不小于MINIMAX，则后面的元素均可以按照从小到大的顺序排在$x_i$的后面，此时所有元素都在第一个归并段中，此时第一个归并段的长度为$n$，显然这也是第一个归并段的长度的最大值。

若原来的文件中$x_1$、$x_2$、$\cdots$、$x_m$是最大的$m$个元素，则将这$m$个元素中的任意一个作为MINIMAX时，后面的文件记录在归并段中均无法位于前面$m$个元素的后面，也就无法与前面$m$个元素位于同一个归并段中，此时第一个归并段的长度为$m$，显然这也是第一个归并段的长度的最小值。

故第（2）问的答案为：生成的第一个归并段的长度的最大值为$n$，最小值为$m$。

计算机与安全理论
赏
评论